Introducing the Pythagorean Theorem and Special Right Triangles Answer Key, a comprehensive resource that unlocks the secrets of this fundamental mathematical concept. This guide provides a thorough exploration of the theorem, its applications, and the special right triangles associated with it, empowering you with the knowledge to solve a wide range of geometric problems.
Delving into the Pythagorean theorem’s history, applications, and significance, this guide unveils the elegance and practicality of this mathematical cornerstone. Discover the relationships between the sides of special right triangles, unravel the theorem’s extension into higher dimensions, and witness its role in mathematical proofs and problem-solving.
Pythagorean Theorem and Special Right Triangles
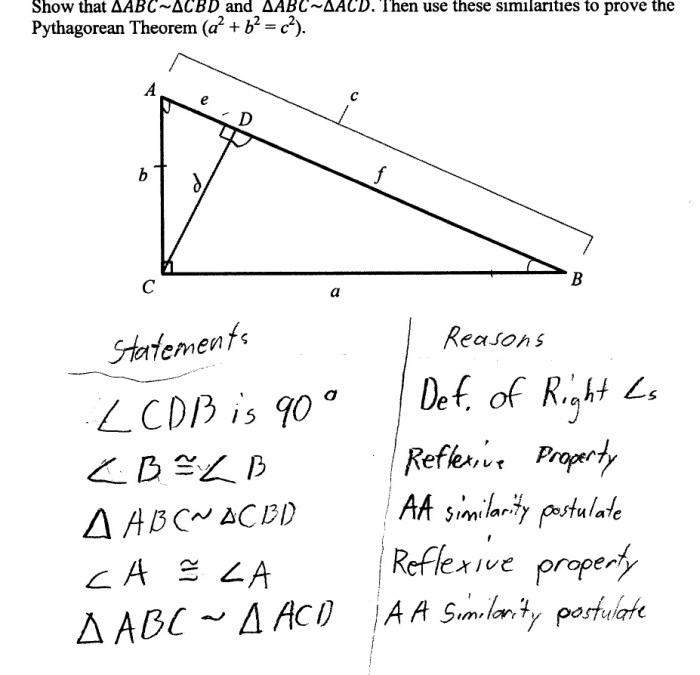
The Pythagorean theorem is a fundamental theorem in geometry that states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.
The theorem is often written as the equation a2+ b2= c2, where aand bare the lengths of the legs of the right triangle and cis the length of the hypotenuse.
The Pythagorean theorem has been known for thousands of years and has been used to solve a wide variety of problems in geometry, architecture, and other fields. The theorem is named after the Greek mathematician Pythagoras, who is credited with first discovering it.
Special Right Triangles
There are three special right triangles that have integer side lengths: the 3-4-5 triangle, the 5-12-13 triangle, and the 8-15-17 triangle. These triangles are known as Pythagorean triples, and they have the property that the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides.
The 3-4-5 triangle is the most well-known Pythagorean triple, and it is often used as an example in geometry problems. The other two Pythagorean triples, the 5-12-13 triangle and the 8-15-17 triangle, are also used in a variety of applications.
Applications in Geometry, Pythagorean theorem and special right triangles answer key
The Pythagorean theorem is used to solve a wide variety of problems in geometry. For example, the theorem can be used to find the length of the hypotenuse of a right triangle, the length of a side of a right triangle, or the area of a right triangle.
The Pythagorean theorem can also be used to solve problems involving other geometric shapes, such as squares, rectangles, and circles. For example, the theorem can be used to find the length of the diagonal of a square or the radius of a circle.
Applications in Real-World Scenarios
The Pythagorean theorem has a wide variety of applications in real-world scenarios. For example, the theorem is used in architecture to calculate the height of a building or the length of a roof. The theorem is also used in engineering to calculate the strength of a bridge or the load-bearing capacity of a structure.
The Pythagorean theorem is also used in surveying to measure the distance between two points. The theorem can also be used to find the height of a tree or the depth of a well.
Advanced Concepts
The Pythagorean theorem can be extended to higher dimensions. For example, the Pythagorean theorem can be used to find the distance between two points in three-dimensional space. The theorem can also be used to find the volume of a three-dimensional object.
The Pythagorean theorem is related to other mathematical concepts, such as trigonometry and calculus. The theorem can be used to derive trigonometric identities and to solve calculus problems.
Expert Answers: Pythagorean Theorem And Special Right Triangles Answer Key
What is the Pythagorean theorem?
The Pythagorean theorem states that in a right triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.
What are the three special right triangles?
The three special right triangles are the 3-4-5 triangle, the 5-12-13 triangle, and the 8-15-17 triangle.
How can I use the Pythagorean theorem to solve real-world problems?
The Pythagorean theorem can be used to solve a wide range of real-world problems, such as finding the height of a building, the distance to a star, or the length of a shadow.