Chapter 6 quadrilaterals answer key – Step into the captivating world of quadrilaterals with our comprehensive answer key for Chapter 6. Embark on an enlightening journey where we decipher the mysteries of these geometric wonders, unraveling their properties, formulas, and applications in a way that will ignite your curiosity and deepen your understanding.
From the fundamental concept of quadrilaterals to the intricacies of their diagonals, we delve into every aspect, providing you with a solid foundation in this fascinating topic.
Chapter 6 Quadrilaterals Answer Key
Quadrilaterals are two-dimensional shapes with four sides and four angles. They come in various forms, each with unique properties and characteristics.
The following table provides an overview of different types of quadrilaterals, their properties, and examples:
| Type | Properties | Examples |
|---|---|---|
| Square | Four equal sides, four right angles | Rubik’s Cube, playing dice |
| Rectangle | Four right angles, opposite sides equal | Books, doors, windows |
| Parallelogram | Opposite sides parallel, opposite angles equal | Notebooks, solar panels |
| Rhombus | Four equal sides, opposite angles equal | Kite, diamond ring |
| Trapezoid | One pair of parallel sides | Traffic signs, roof tiles |
| Kite | Two pairs of adjacent sides equal | Airplanes, flags |
Common Formulas Related to Quadrilaterals
The following formulas are commonly used to calculate the area, perimeter, and diagonals of quadrilaterals:
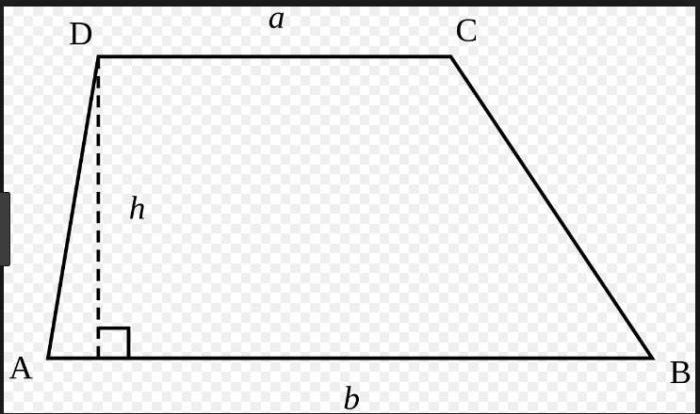
- Area:For a rectangle or parallelogram, Area = length × width. For a trapezoid, Area = 1/2 × (base1 + base2) × height.
- Perimeter:Perimeter = sum of all four sides
- Diagonals:For a parallelogram, diagonals bisect each other. For a rhombus, diagonals are perpendicular and bisect each other.
Properties of Quadrilaterals: Chapter 6 Quadrilaterals Answer Key
Quadrilaterals are polygons with four sides and four angles. They come in various shapes and sizes, each with its unique set of properties. Some of the most common quadrilaterals include parallelograms, rectangles, and squares.
Properties of Parallelograms, Chapter 6 quadrilaterals answer key
Parallelograms are quadrilaterals with opposite sides parallel and congruent. This means that the opposite sides of a parallelogram are equal in length and run parallel to each other. Additionally, the opposite angles of a parallelogram are congruent, meaning they have the same measure.
Properties of Rectangles
Rectangles are a specific type of parallelogram with four right angles. This means that all four angles of a rectangle measure 90 degrees. In addition to having opposite sides parallel and congruent, rectangles also have diagonals that are perpendicular to each other.
Properties of Squares
Squares are a special type of rectangle with all four sides congruent. This means that all four sides of a square have the same length. In addition to having four right angles and perpendicular diagonals, squares also have four congruent angles, each measuring 90 degrees.
Area and Perimeter of Quadrilaterals
In geometry, the area of a figure is the measure of its surface, while the perimeter is the distance around its boundary. Quadrilaterals are polygons with four sides, and their area and perimeter can be calculated using specific formulas.
Parallelograms
A parallelogram is a quadrilateral with two pairs of parallel sides. The area of a parallelogram is calculated by multiplying the length of its base by its height. The perimeter is calculated by adding the lengths of all four sides.
Area: A = b
h
Perimeter: P = 2(b + h)
Rectangles
A rectangle is a parallelogram with four right angles. The area of a rectangle is calculated by multiplying its length by its width. The perimeter is calculated by adding the lengths of all four sides.
Area: A = l
w
Perimeter: P = 2(l + w)
Squares
A square is a rectangle with all four sides equal. The area of a square is calculated by squaring its side length. The perimeter is calculated by multiplying the side length by 4.
Area: A = s^2Perimeter: P = 4s
Examples
| Quadrilateral | Formula | Example |
|---|---|---|
| Parallelogram | A = b
|
A parallelogram with a base of 5 cm and a height of 3 cm has an area of 15 cm2. |
| Rectangle | A = l
|
A rectangle with a length of 6 cm and a width of 4 cm has an area of 24 cm2. |
| Square | A = s^2 | A square with a side length of 5 cm has an area of 25 cm2. |
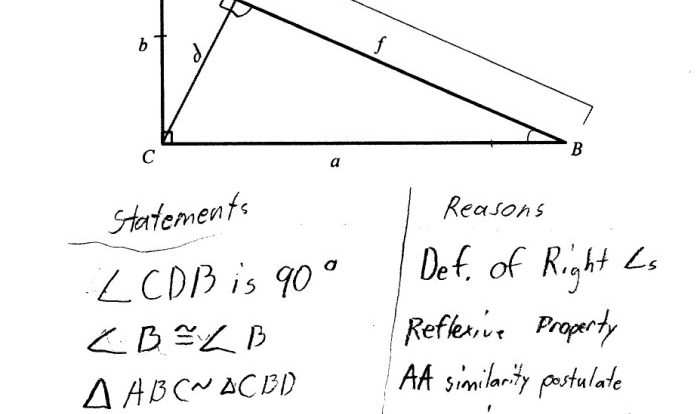
Diagonals of Quadrilaterals
In a quadrilateral, a diagonal is a line segment that connects two non-adjacent vertices. Quadrilaterals can have two diagonals, and the properties of these diagonals depend on the type of quadrilateral.
In a parallelogram, the diagonals bisect each other. This means that they divide each other into two equal segments. The diagonals of a parallelogram also divide the parallelogram into four congruent triangles.
Properties of Diagonals in Rectangles
In a rectangle, the diagonals are perpendicular to each other. This means that they form a right angle when they intersect. The diagonals of a rectangle are also congruent, meaning they have the same length.
Applications of Quadrilaterals
Quadrilaterals are a fundamental geometric shape with numerous applications in everyday life. Their unique properties make them suitable for various fields, including architecture, design, and engineering.
In architecture, quadrilaterals form the basis of many structural elements. Rectangles are commonly used in building walls, ceilings, and floors due to their stability and ease of construction. Squares, with their equal sides and right angles, are often used in windows, doors, and other decorative elements.
Design
In design, quadrilaterals play a crucial role in creating visually appealing and functional spaces. Rectangles and squares are commonly used in furniture design, providing a sense of balance and symmetry. Trapezoids and parallelograms are often used in interior design to create dynamic and interesting shapes.
Engineering
In engineering, quadrilaterals are used in the design and construction of bridges, buildings, and other structures. Rectangles and squares are used in the framework of bridges, providing stability and strength. Parallelograms are used in trusses, a type of structural framework, to distribute weight evenly.
Careers Involving Quadrilaterals
Working with quadrilaterals is a part of various careers, including:
- Architect
- Interior Designer
- Structural Engineer
- Civil Engineer
- Product Designer
Key Questions Answered
What is the definition of a quadrilateral?
A quadrilateral is a two-dimensional figure with four straight sides and four angles.
How do you calculate the area of a parallelogram?
Area = base × height
What is the relationship between the diagonals of a rectangle?
The diagonals of a rectangle are perpendicular and congruent.